Wpisz się do mojej księgi gości!
PRZEKSZTAŁCENIA GEOMETRYCZNE SYMETRIE
Co to jest symetria?
Symetria figury- każda taka izomeria, która przekształca
figurę na tę samą figurę, tzn. przeprowadza każdy punkt figury na pewien punkt
tej figury.
Nie musi być to symetria płaszczyznowa, osiowa czy punktowa.
Wszystkie symetrie danej figury tworzą grupę, tzn.
1) przekształcenie tożsamościowe jest symetrią figury,
2) złożenie dwóch symetrii figury jest symetrią tej figury,
3) przekształcenie odwrotne do symetrii figury jest symetrią tej figury.
Grupa symetrii wielościanu jest zbiorem o skończonej liczbie elementów, tzn.
każdy wielościan ma skończoną liczbę symetrii, która nie może być większa od k,
gdzie k oznacza liczbę wierzchołków wielościanu.
Jeżeli
figura jest symetryczna sama do siebie względem pewnej prostej, to tę prostą
nazywamy osią symetrii figury, a figurę nazywamy osiowosymetryczna.
Przykłady
osi symetrii:
Dla figur płaskich i przestrzennych w zależności od
rodzaju przekształcenia wyróżniana jest m.in.:
symetria
osiowa – przekształceniem jest odbicie zwierciadlane figury płaskiej
względem zadanej prostej
zwanej osią symetrii. Symetria osiowa występuje m.in. w
trójkącie Sierpińskiego.
symetria
płaszczyznowa – przekształceniem jest odbicie zwierciadlane figury względem płaszczyzny
zwanej płaszczyzną symetrii. Symetria płaszczyznowa
występuje m.in. w piramidzie Sierpińskiego oraz kostce Mengera.
symetria
z obrotem (zwierciadlano-obrotowa) – na płaszczyźnie jest
to złożenie symetrii względem prostej z obrotem o dowolny kąt wokół zadanego
punktu. W przestrzeni jest złożeniem symetrii płaszczyznowej z obrotem wokół
prostej (symetria cylindryczna). [Niektóre pozycje książkowe podają, że
w przestrzeni oś obrotu musi być prostopadła do płaszczyzny symetrii.]
symetria
sferyczna – przekształceniem jest dowolny obrót bryły wokół
zadanego punktu. Własność tę posiada m.in. kula.
symetria środkowa
– na płaszczyźnie złożenie dwóch symetrii osiowych o prostopadłych osiach (lub
obrót o kąt 180 stopni), w przestrzeni - trzech symetrii płaszczyznowych o
wzajemnie prostopadłych płaszczyznach symetrii.
symetria
parzysta – złożenie parzystej liczby symetrii osiowych (na
płaszczyźnie) lub płaszczyznowych (w przestrzeni). Przykładem jest symetria
środkowa (złożenie dwóch prostopadłych osi symetrii).
symetria
nieparzysta – złożenie nieparzystej liczby symetrii osiowych (na
płaszczyźnie) lub płaszczyznowych (w przestrzeni).
symetria
ukośna – uogólnienie symetrii osiowej. Jeśli dane są dwie
proste k i m przecinające się pod kątem α, oraz dany jest
odcinek AB, to symetria ukośna względem prostej k, w kierunku
prostej m, polega na tym, że przez punkty A i B prowadzimy
proste a i b równoległe do prostej m, przecinające prostą k
odpowiednio w punktach K1 i K2, i znajdujemy na nich punkty A’
i B’ w taki sposób, że odległość od punktu A do K1 jest
równa odległości od punktu K1 do A’ oraz analogicznie |BK2|
= |K2B |.
Przykład symetrii osiowej

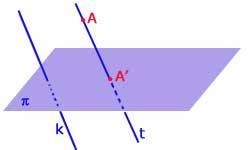
Przykład symetrii płaszczyznowej
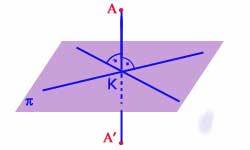
Przykład symetrii rzutem równoległym na płaszczyznę